General Theory of Relativity GTR - Všeobecná teória relativity
Gravitácia a zakrivenie priestoru
- Hmota (presnejšie jej energia a hybnosť) zakrivuje časopriestor vo svojom okolí.
- Predmet, na ktorý nepôsobí žiadna sila, sa pohybuje medzi dvoma miestami časopriestoru vždy po najpriamočiarejšej trajektórii, takzvanej geodetickej čiare.
Prvá výpoveď opisuje pôsobenie energie a hybnosti na časopriestor, druhá naopak – ide teda o vzájomné pôsobenie (interakciu) v pravom slova zmysle.
Už štvorrozmerný časopriestor špeciálnej teórie relativity sa dá ťažko názorne predstaviť – pri zakrivenom časopriestore je to o to ťažšie. V záujme predstavivosti si však možno pozrieť situácie so zníženým počtom rozmerov. Napríklad v prípade dvojrozmernej zakrivenej krajiny zodpovedá najpriamejšej trajektórii, ktorú by prešlo vozidlo s riadením zafixovaným na jazdu rovno vpred. Ak by dve takéto vozidlá odštartovali na rovníku paralelne smerom na sever, stretli by sa na severnom póle. Pozorovateľ, ktorý by nevedel o guľovom tvare Zeme, by z toho vyvodil, že medzi dvomi vozidlami existuje príťažlivá sila. V skutočnosti ide o geometrický jav (guľatosť Zeme). Gravitačné sily sa preto niekedy označujú aj ako zdanlivé sily.
https://sk.wikipedia.org/wiki/Všeobecná_teória_relativity
https://en.wikipedia.org/wiki/General_relativity
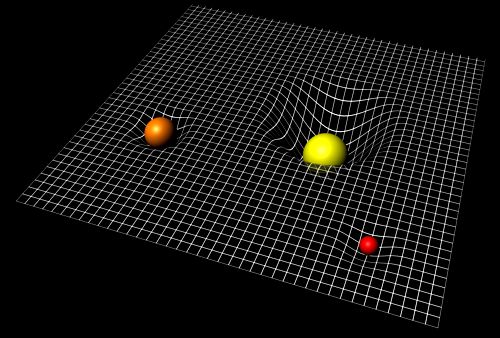
V našich pozemských gravitačných podmienkach sa to názorne dá ilustrovať pomocou vodorovne napnuté pružnej plachty (ktorá predstavuje nezakrivený priestor bez gravitácie), na ktorú položíme hmotnú guľu M.
Zaťažením vzniknutá priehlbina predstavuje zakrivenie priestoru. Keď sem položíme menšie guličku m1, skotúľa sa do priehlbiny a dopadne na väčšiu guľu. Ak však guľôčke m2 udelíme vhodnú obvodovú rýchlosť, bude obiehať okolo ťažké gule, ktorá je zdrojom zakrivenie, podobne ako planéta obieha okolo gravitující hviezdy alebo mesiac-satelit okolo planéty. Pri vyššej rýchlosti guľôčky m3 sa jej dráha v priehlbine len zakriví a gulička pokračuje v pohybe pod iným uhlom.
Podobne, hladké a symetrické teleso (ako je guľa), rotujúce v ideálnej kvapaline bez viskozity, nespôsobuje pohyb kvapaliny vo svojom okolí.
Vpravo: Vo všeobecnej teórii relativity však rotácie zdroje zanecháva na vonkajšom gravitačnom poli (na metrike časopriestore) charakteristické "stopy" - dochádza k strhávaniu lokálnych inerciálnych sústav - strhávanie voľných telies rotujúcim gravitačným poľom do smeru rotácie zdroja.
Podobne, teleso rotujúce vo viskóznej kvapaline strháva do rotácie kvapalinu v blízkosti svojho povrchu.
Einsteinove rovnice je možné zapísať v tvare
https://en.wikipedia.org/wiki/General_relativity
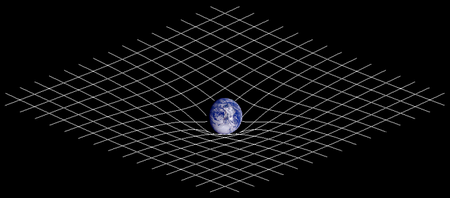
Hmotné teleso vo svojom okolí zakrivuje časopriestor
(Príklad sféricky symetrického telesa)
Zaťažením vzniknutá priehlbina predstavuje zakrivenie priestoru. Keď sem položíme menšie guličku m1, skotúľa sa do priehlbiny a dopadne na väčšiu guľu. Ak však guľôčke m2 udelíme vhodnú obvodovú rýchlosť, bude obiehať okolo ťažké gule, ktorá je zdrojom zakrivenie, podobne ako planéta obieha okolo gravitující hviezdy alebo mesiac-satelit okolo planéty. Pri vyššej rýchlosti guľôčky m3 sa jej dráha v priehlbine len zakriví a gulička pokračuje v pohybe pod iným uhlom.
Hydrodynamická analógia vplyvu rotácie zdrojového telesa na vlastnosti budeného gravitačného poľa.
Vľavo: V rámci Newtonovej teórie je gravitačné pole telesa dané iba rozložením hmoty a vôbec nezávisí na jeho prípadnej rotácii (pokiaľ však táto nevedie k zmenám distribúcie hmoty).Podobne, hladké a symetrické teleso (ako je guľa), rotujúce v ideálnej kvapaline bez viskozity, nespôsobuje pohyb kvapaliny vo svojom okolí.
Vpravo: Vo všeobecnej teórii relativity však rotácie zdroje zanecháva na vonkajšom gravitačnom poli (na metrike časopriestore) charakteristické "stopy" - dochádza k strhávaniu lokálnych inerciálnych sústav - strhávanie voľných telies rotujúcim gravitačným poľom do smeru rotácie zdroja.
Podobne, teleso rotujúce vo viskóznej kvapaline strháva do rotácie kvapalinu v blízkosti svojho povrchu.
Vo všeobecnej relativite samé telesa zakrivujú čas a priestor a v tomto zakrivenom časopriestore sa pohybujú po najrovnejších možných dráhach - geodetikách. Napríklad voľný pád všetkých telies prebieha rovnako preto, že sa pohybujú v časopriestore zakrivenom Zemou a toto zakrivenie je pre všetky telesá rovnaké.
Priestor a čas v všeobecnej relativite bez samotných telies neexistujú. Telesá sama časopriestor vytvárajú. Zakrivenie časopriestoru je matematicky popisované metrickým tenzorom - ide vlastne o koeficienty gμν v Pythagorovej vete, ktoré určujú vlastnosti času a priestoru.
| Základní metriky | |
|---|---|
| dl2 = dx2 + dy2 + dz2 | Kartézská metrika – kvadrát vzdálenosti v kartézském souřadnicovém systému. |
| ds2 = −c2dt2 + dx2 + dy2 + dz2 | Minkowského metrika – časoprostorový interval ve speciální relativitě. |
| ds2 = g00dt2 + g11dx2 + g22dy2 + g33dz2 | Riemannova metrika – metrika v obecné relativitě (v ortogonálním systému souřadnic). |
Každé teleso okolo seba zakrivuje a spoluvytvára čas a priestor.
1. Každé teleso zakrivuje priestor a čas okolo seba.
2. V tomto pokrivenom svete sa telesá pohybujú po najrovnejší možných dráhach (geodetikách).
Telesá časopriestor sami vytvárajú, bez nich časopriestor neexistuje a nemá zmysel.
Některé užitečné vztahy
| Δω/ω0 = –Δλ/λ0 = Δϕ/c2 | Změna frekvence fotonu způsobená změnou gravitačního potenciálu ϕ. V tíhovém poli je Δϕ = gΔl. |
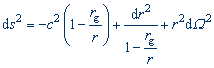 | Schwarzschildova metrika. Tvar intervalu ve sférických souřadnicích v okolí sféricky symetrického tělesa. |
| rg = 2GM/c2 | Schwarzschildův poloměr. Poloměr, z pod kterého se od hmotného tělesa nemůže vzdálit ani světlo |
| M, L, Q = const | „No hair“ teorém. Černá díra si ponechává jen informaci o hmotnosti, momentu hybnosti a náboji |
| ΣSk(t) ≤ ΣSk(t+Δt) | Termodynamika černých děr. Ať probíhají jakékoli procesy včetně spojování černých děr, celkový povrch se nezmenší. Povrch černé díry v jistém smyslu představuje pojem entropie klasického souboru částic |
| Fridmanova-Lemaitre-Robertsonova-Walkerova metrika rozpínajícího se vesmíru | |
| H2 – 8/3 πGρ = –c2k/a2 | Einsteinova-Fridmanova rovnice. Diferenciální rovnice pro expanzní funkci a(t). Veličina k je křivost vesmíru. |
| H ≡ (da/dt)/a | Hubblova konstanta. Udává koeficient úměrnosti mezi rychlostí rozpínání vesmíru a vzdáleností objektu.Z pozorování: H ~ (68±4) km s−1 Mpc−1. |
| ρC = 3H2/(8πG) | Kritická hustota. Hustota, při níž se ve Fridmanově řešení mění otevřený (stále se rozpínající) vesmír na uzavřený (v budoucnu kolabující). |
| z = Δλ/λ0 = [a(t) – a(t0)]/a(t0) | Kosmologický posuv. Změna frekvence vyzařovaného světla způsobená změnou geometrie prostředí, kterým se světlo šíří, tedy rozpínáním vesmíru. |
SKLADANIE RÝCHLOSTÍ
Z klasickej fyziky platí, že výsledná rýchlosť sa rovná súčtu rýchlosti pohybujúceho sa telesa /u/ a rýchlosti objektu vo vnútri tohto telesa /v/ :
platnosť tohto vzťahu pre u = c (c - rýchlosť svetla)
http://edu.techmania.cz/cs/encyklopedie/fyzika/teorie-relativity/zakladni-principy/skladani-rychlosti
RNDr. Robert Švarc, Ph.D., Obecná teorie relativity: Gravitace podle Einsteina











Komentáre
Zverejnenie komentára